Elbow Manipulator Simulation
Introduction
It was shown in 1985 that the elbow manipulator is the “optimal” 6R manipulator. Because of this, the elbow manipulator has been employed often in usage scenarios all around the world. It is also one of the most recognized forms of a manipulator. Because of the importance of the elbow manipulator to the field of kinematics, it is useful to simulate such a manipulator and its motion. This project tackles the regional problem of the elbow manipulator; the simulation attempts to find the necessary angles to move the manipulator to the desired location from its current position. The simulation does not yet analyze any orientation issues that can be accomplished with the last three revolute joints in the standard 6R manipulator.
In order to demonstrate the motion of the elbow manipulator, a series of random points are chosen within the manipulator’s workspace. Then, starting from the “home” position of the manipulator, the joints are moved to have the tool frame at the end of the last link coincide with the desired location. Once the target location is reached, the target is then moved to the next location. Recalculation of the new path is done, and the manipulator once again moves to the desired location.
Special care was taken to account for a difference of a multiple of 2π in the angles. Despite being on different complex planes, the manipulator resides only in the real space, so care is taken to normalize the variables to find the shortest path. In addition, the manipulator simulation is realistic in that the links will not collide with each other. Though nearly physically impossible, the joints are given a full range of motion that is theoretically possible. This is, the manipulator in the simulation is not hampered by mechanical limitations, as a simulation should be.
Code
Main method
clear all; close all; clc; % Height of shoulder to base H = 15; % Arm lengths L1 = 8; % Upper arm L2 = 5; % Forearm % Arm thickness (radius) r = 0.2; % Desired position of tool frame % Tool frame at end of forearm (where wrist would be) p_d = [-5; -5; 19]; % Prompt for user given desired position % p_d(1) = str2double(input('X-value: ', 's')); % if isempty(p_d(1)) % p_d(1) = (L1+L2)/2; % end % p_d(2) = str2double(input('Y-value: ', 's')); % if isempty(p_d(2)) % p_d(2) = (L1+L2)/2; % end % p_d(3) = str2double(input('Z-value: ', 's')); % if isempty(p_d(3)) % p_d(3) = H; % end % Initial joint angles theta_current = [0; 0; 0]; % Initialize variables fig = figure; theta_d = zeros(3,1); robot = zeros(4,1); [sphere_x, sphere_y, sphere_z] = sphere(20); desired_point = surf(1e-5*sphere_x, 1e-5*sphere_y, 1e-5*sphere_z); set(desired_point, 'XData', 0.25*sphere_x + p_d(1), 'YData', 0.25*sphere_y + p_d(2), 'ZData', 0.25*sphere_z + p_d(3)); set(desired_point, 'EdgeColor', 'none', 'FaceColor', 'red'); % Set up figure axis([-(L1+L2) (L1+L2) -(L1+L2) (L1+L2) 0 (L1+L2)+H]); grid on; view(36,45); xlabel('x'); ylabel('y'); zlabel('z'); % Display static text (for joint angles and target position) angle_str = {{},{},{}}; for angle=1:3 angle_str(angle) = {['\theta_' num2str(angle) ' = ']}; end text(0,0, angle_str, 'Units', 'pixels'); point_str = {'x^D = ','y^D = ','z^D = '}; text(385,0, point_str, 'Units', 'pixels'); for run=1:100 % Calculate a random desired point p_d = rand(3,1); a = ((L1+L2) - abs(L2-L1)) * p_d(1) + abs(L2-L1); b = p_d(2) * 2*pi; c = p_d(3) * pi; p_d(1) = a * cos(b) * sin(c); p_d(2) = a * sin(b) * sin(c); p_d(3) = max(0, a * cos(c) + H); % Plot desired point as sphere if desired_point == 0 desired_point = surf(0.25*sphere_x + p_d(1), 0.25*sphere_y + p_d(2), 0.25*sphere_z + p_d(3)); else set(desired_point, 'XData', 0.25*sphere_x + p_d(1), 'YData', 0.25*sphere_y + p_d(2), 'ZData', 0.25*sphere_z + p_d(3)); end set(desired_point, 'EdgeColor', 'none', 'FaceColor', 'red'); % Calculate desired end theta % Check that the desired position is reachable if norm(p_d - [0; 0; H]) <= (L1 + L2) && norm(p_d - [0; 0; H]) >= (abs(L1 - L2)) % Solve for 2 solutions for theta_3 temp = acos((norm(p_d - [0;0;H])^2 - L1^2 - L2^2)/(2*L1*L2)); theta_3 = [temp; -temp]; % Solve for 2 solutions for theta_2 for EACH theta_3 % theta_3(1) -> theta_2(1,:) theta_2 = zeros(2,2); for i=1:2 r_H = norm([p_d(1); p_d(2)]); a = r_H + (L1 + L2*cos(theta_3(i))); b = 2 * L2 * sin(theta_3(i)); c = r_H - (L1 + L2 * cos(theta_3(i))); theta_2(i,1) = 2 * atan(real((-b + sqrt(b^2 - 4*a*c)) / (2 * a))); theta_2(i,2) = 2 * atan(real((-b - sqrt(b^2 - 4*a*c)) / (2 * a))); end % Solve for theta_1 for each pair of theta_2 and theta_3 theta_1 = zeros(2,2); for i=1:2 for j=1:2 temp = L1 * cos(theta_2(i,j)) + L2 * cos(theta_2(i,j) + theta_3(i)); theta_1(i,j) = atan2(p_d(2) / temp, p_d(1) / temp); end end % Gather all pairs of thetas theta = zeros(4,3); for i=1:4 theta(i,1) = theta_1(floor((i-1)/2)+1, mod(i-1,2)+1); theta(i,2) = theta_2(floor((i-1)/2)+1, mod(i-1,2)+1); theta(i,3) = theta_3(floor((i-1)/2)+1); g_base_wrist = g_transform(0,0,H,0) * g_transform(0,0,0,theta(i,1)) * g_transform(0,-pi/2,0,theta(i,2)) * g_transform(L1,0,0,theta(i,3)) * g_transform(L2,0,0,0); [~,d] = g_to_vector(g_base_wrist); % Use correction to accommodate flipping over itself if norm(d - p_d) > 1e-4 theta(i,1) = theta(i,1) + pi; theta(i,2) = theta(i,2) + pi; end end % Change joint angles to be on same revolution as current angles for i=1:4 if abs(theta(i,1) - theta_current(1)) > pi if theta_current(1) > 0 theta(i,1) = theta(i,1) + 2*pi; else theta(i,1) = theta(i,1) - 2*pi; end end if theta(i,2) > pi/2 theta(i,2) = theta(i,2) - 2*pi; end end % Check for collisions % Once joint angles are normalized, only collision could be between % last link and base link for i=4:-1:1 [~,d_base_wrist] = g_to_vector(g_transform(0,0,H,0) * g_transform(0,0,0,theta(i,1)) * g_transform(0,-pi/2,0,theta(i,2)) * g_transform(L1,0,0,theta(i,3)) * g_transform(L2,0,0,0)); [~,d_base_elbow] = g_to_vector(g_transform(0,0,H,0) * g_transform(0,0,0,theta(i,1)) * g_transform(0,-pi/2,0,theta(i,2)) * g_transform(L1,0,0,theta(i,3))); d_base_wrist = d_base_wrist'; d_base_elbow = d_base_elbow'; if d_base_wrist(3) < H if sign(d_base_wrist(1)) ~= sign(d_base_elbow(1)) || sign(d_base_wrist(2)) ~= sign(d_base_elbow(2)) theta(i,:) = []; end end end % Determine closest set of desired theta delta_theta = zeros(size(theta,1),1); for sol=1:size(theta,1) delta_theta(sol) = norm(theta(sol,:)' - theta_current(:))^2; end [~, I] = min(delta_theta); theta_d = theta(I,:)'; end % Plot the robot theta_start = theta_current; T = 1; dt = 0.025; % keep above about 0.02 to keep animation in real time robot = plot_elbow(H, L1, L2, r, theta_current, robot); % Draw the values of the joint angles and target coordinates to the plot angle_str = {{},{},{}}; text_angles = zeros(3,1); for angle=1:3 angle_str(angle) = {num2str(round(rad2deg(theta_current(angle))))}; text_angles(angle) = text(55,43-21*angle, angle_str(angle), 'Units', 'pixels', 'HorizontalAlignment', 'Right'); end point_str = {{};{};{}}; text_point = zeros(3,1); for coord=1:3 point_str(coord) = {num2str(p_d(coord))}; text_point(coord) = text(475,43-21*coord, point_str(coord), 'Units', 'pixels', 'HorizontalAlignment', 'Right'); end pause(0.1); % Clear current text of joint angles (since it changes with each timestep) delete(text_angles); for t=0:dt:T tic theta_current = (theta_d - theta_start) * t/T + theta_start; robot = plot_elbow(H, L1, L2, r, theta_current, robot); % Draw the values of the joint angles to the plot angle_str = {{},{},{}}; text_angles = zeros(3,1); for angle=1:3 angle_str(angle) = {num2str(round(rad2deg(theta_current(angle))))}; text_angles(angle) = text(55,43-21*angle, angle_str(angle), 'Units', 'pixels', 'HorizontalAlignment', 'Right'); end % Wait rest of timestep to keep as close to realtime as possible elapsed_time = toc; pause(dt - elapsed_time); % Clear current text displaying joint angles delete(text_angles); end % Clear the current text of target coordinates delete(text_point); % Normalize joint angles % theta_1 = [-pi, pi] % theta_2 = [-3*pi/2, pi/2] % theta_3 = [-pi, pi] while theta_current(1) < -pi || theta_current(1) > pi theta_current(1) = theta_current(1) + (-sign(theta_current(1))) * 2*pi; end while theta_current(2) < -3*pi/2 || theta_current(2) > pi/2 theta_current(2) = theta_current(2) + (-sign(theta_current(2))) * 2*pi; end while theta_current(3) < -pi || theta_current(3) > pi theta_current(3) = theta_current(3) + (-sign(theta_current(3))) * 2*pi; end end
Plotting function
function [robot] = plot_elbow(H, L1, L2, r, theta_current, robot) g_base_shoulder = g_transform(0,0,H,0); g_shoulder_elbow = g_transform(0,0,0,theta_current(1)) * g_transform(0,-pi/2,0,theta_current(2)) * g_transform(L1,0,0,theta_current(3)); g_elbow_wrist = g_transform(L2,0,0,0); % Find displacement relative to base of each joint D = zeros(4,3); [~,d] = g_to_vector(g_base_shoulder); D(2,:) = d'; [~,d] = g_to_vector(g_base_shoulder * g_shoulder_elbow); D(3,:) = d'; [~,d] = g_to_vector(g_base_shoulder * g_shoulder_elbow * g_elbow_wrist); D(4,:) = d'; % Plot the arm for i=1:size(D,1)-1 % Create unit vector of link vector = D(i+1,:) - D(i,:); vector = vector ./ norm(vector); % Find w vector and angle to rotate circle about % so circle will be perpendicular to link vector w = cross([0,0,1], vector); phi = atan2(norm(cross([0,0,1],vector)),dot([0,0,1],vector)); % Create rotation vector to rotate circle of link w_hat = [0,-w(3),w(2);w(3),0,-w(1);-w(2),w(1),0]; R = expm(phi*w_hat); % Define points of circle for arm vertices % resolution is number of points for the circle on ends of links resolution = 12; vertices = zeros(resolution*2,3); vertices(1:size(vertices,1)/2,1) = r*cos(0:2*pi/(size(vertices,1)/2):2*pi-2*pi/(size(vertices,1)/2)); vertices(1:size(vertices,1)/2,2) = r*sin(0:2*pi/(size(vertices,1)/2):2*pi-2*pi/(size(vertices,1)/2)); vertices(1:size(vertices,1)/2,3) = zeros(size(vertices,1)/2,1); vertices(size(vertices,1)/2+1:end,1) = r*cos(0:2*pi/(size(vertices,1)/2):2*pi-2*pi/(size(vertices,1)/2)); vertices(size(vertices,1)/2+1:end,2) = r*sin(0:2*pi/(size(vertices,1)/2):2*pi-2*pi/(size(vertices,1)/2)); vertices(size(vertices,1)/2+1:end,3) = zeros(size(vertices,1)/2,1); % Rotate vertices to match direction of link for j=1:size(vertices,1) vertices(j,:) = (R * vertices(j,:)')'; end % Move vertices to be at placement of link vertices(1:size(vertices,1)/2,1) = vertices(1:size(vertices,1)/2,1) + D(i,1); vertices(1:size(vertices,1)/2,2) = vertices(1:size(vertices,1)/2,2) + D(i,2); vertices(1:size(vertices,1)/2,3) = vertices(1:size(vertices,1)/2,3) + D(i,3); vertices(size(vertices,1)/2+1:end,1) = vertices(size(vertices,1)/2+1:end,1) + D(i+1,1); vertices(size(vertices,1)/2+1:end,2) = vertices(size(vertices,1)/2+1:end,2) + D(i+1,2); vertices(size(vertices,1)/2+1:end,3) = vertices(size(vertices,1)/2+1:end,3) + D(i+1,3); % Create array of faces that define the link faces = zeros(size(vertices,1)/2+2, max(size(vertices,1)/2, 4)); for j=1:size(vertices,1)/2 faces(j,1:4) = [j, mod(j, size(vertices,1)/2)+1, mod(j, size(vertices,1)/2)+1+size(vertices,1)/2, j+size(vertices,1)/2]; if size(vertices,1)/2 > 4 faces(j,5:end) = NaN(1, size(faces,2)-4); end end faces(size(vertices,1)/2+1, 1:size(vertices,1)/2) = 1:size(vertices,1)/2; faces(size(vertices,1)/2+2, 1:size(vertices,1)/2) = size(vertices,1)/2+1:size(vertices,1); if size(vertices,1)/2 < size(faces,2) faces(size(faces,1)-1:end, size(vertices,1)/2+1:end) = NaN(2, size(faces,2)-size(vertices,1)/2); end % Draw 3D link color = [0.5, 0.5, 1.0]; if robot(i) == 0 robot(i) = patch('Vertices',vertices,'Faces',faces,'FaceColor',[0.5,0.5,1.0],'EdgeColor',0.5*color); else set(robot(i), 'Vertices',vertices,'Faces',faces,'FaceColor',[0.5,0.5,1.0],'EdgeColor',0.5*color); end hold on; end drawnow; end
Helper functions
function [R, d] = g_to_vector(g) d = g(1:3,4); R = g(1:3,1:3); end function [g] = g_transform(a, alpha, d, theta) g = [cos(theta), -sin(theta), 0, a; sin(theta)*cos(alpha), cos(theta)*cos(alpha), -sin(alpha), -d*sin(alpha); sin(theta)*sin(alpha), cos(theta)*sin(alpha), cos(alpha), d*cos(alpha); 0, 0, 0, 1 ]; end
Simulation Screenshots

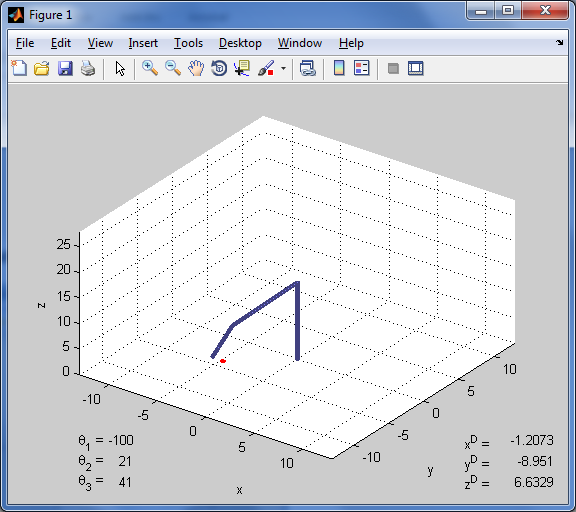


Movement to Reach One Target
The following are screenshots taken at a set interval as the manipulator moves to a specific target.








Conclusion
The project has several shortcomings. First, the manipulator moves linearly between the current location and the final desired location. A much better solution would be to use splines to have a more organic movement that more closely mimics the movement of human limbs. Also, the software does not take into account any possible obstructions (besides itself) that could lie in the path of the manipulator. This can be fixed but requires a far more complex motion planning algorithm beyond the scope of this class.
Additionally, the software is currently written to have a constant time between all pairs of target points. This means that the manipulator will move slowly to a target that is near, while it will race to reach a target on the opposite side of its workspace. This is unrealistic as the joints usually move at or near their maximum speed so as to minimize the total time spent during travel of the manipulator. This can be further improved through the use of the Jacobian matrix to either maximize the overall speed of the tool frame (end of the manipulator) or to maximize the joint rotation speeds. In both cases, the total time to reach the desired location would be dependent on the distance the manipulator needs to travel, as opposed to the current constant time.
Lastly, the graphics are very low quality and each link is represented only by a simple cylinder. While the resolution of the cylinder can be increased, the joints suffer a lack of quality as there becomes space between the cylinders as the joint angles grow. While not important to the final result, this shortcoming affects the overall quality of the simulation. This can be improved with better rendering of the links through a more complicated algorithm that takes into the account the joint angles to match the links to each other and set them flush. Alternatively, an object to represent the joint could be constructed to simulate the physical joint, such as another (perpendicular) cylinder to represent a hinge.
In the end, the project does accomplish its goals. The simulation is easy to run (self-contained MATLAB files) and illustrates how an elbow manipulator moves. Additionally, the randomness of the targets means that the algorithm to both move the robot as well as select the desired joint angles is robust enough to cover the entire workspace. An array of target points could just as easily have been specified instead of a set of random points. With the random points, the code illustrates the workspace of the manipulator as well as shows the robustness of the simulation code.
Home